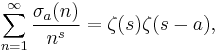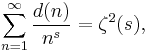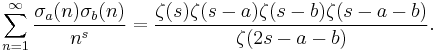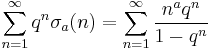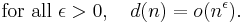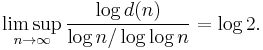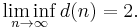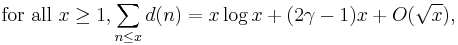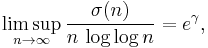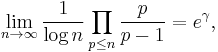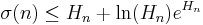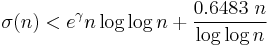Divisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities.
A related function is the divisor summatory function, which, as the name implies, is a sum over the divisor function.
Contents |
Definition
The sum of positive divisors function σx(n), for a real or complex number x, is defined as the sum of the xth powers of the positive divisors of n, or
The notations d(n), ν(n) and τ(n) (for the German Teiler = divisors) are also used to denote σ0(n), or the number-of-divisors function[1][2] (sequence A000005 in OEIS). When x is 1, the function is called the sigma function or sum-of-divisors function,[3][4] and the subscript is often omitted, so σ(n) is equivalent to σ1(n) ( A000203). The aliquot sum s(n) of n is the sum of the proper divisors (that is, the divisors excluding n itself, A001065), and equals σ1(n) − n; the aliquot sequence of n is formed by repeatedly applying the aliquot sum function.
Example
For example, σ0(12) is the number of the divisors of 12:
while σ1(12) is the sum of all the divisors:
and the aliquot sum s(12) of proper divisors is:
Table of values
| n | Divisors | σ0(n) | σ1(n) | s(n) = σ1(n) − n | Comment |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 0 | square number: σ0(n) is odd; power of 2: s(n) = n − 1 (almost-perfect) |
| 2 | 1,2 | 2 | 3 | 1 | |
| 3 | 1,3 | 2 | 4 | 1 | |
| 4 | 1,2,4 | 3 | 7 | 3 | square number: σ0(n) is odd; power of 2: s(n) = n − 1 (almost-perfect) |
| 5 | 1,5 | 2 | 6 | 1 | |
| 6 | 1,2,3,6 | 4 | 12 | 6 | first perfect number: s(n) = n |
| 7 | 1,7 | 2 | 8 | 1 | |
| 8 | 1,2,4,8 | 4 | 15 | 7 | power of 2: s(n) = n − 1 (almost-perfect) |
| 9 | 1,3,9 | 3 | 13 | 4 | square number: σ0(n) is odd |
| 10 | 1,2,5,10 | 4 | 18 | 8 | |
| 11 | 1,11 | 2 | 12 | 1 | |
| 12 | 1,2,3,4,6,12 | 6 | 28 | 16 | first abundant number: s(n) > n |
| 13 | 1,13 | 2 | 14 | 1 | |
| 14 | 1,2,7,14 | 4 | 24 | 10 | |
| 15 | 1,3,5,15 | 4 | 24 | 9 | |
| 16 | 1,2,4,8,16 | 5 | 31 | 15 | square number: σ0(n) is odd; power of 2: s(n) = n − 1 (almost-perfect) |
The cases x=2, x=3 and so on are tabulated in A001157, A001158, A001159, A001160, A013954, A013955 ...
Properties
For a non-square integer every divisor d of n is paired with divisor n/d of n and 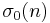 is then even; for a square integer one divisor (namely
is then even; for a square integer one divisor (namely 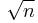 ) is not paired with a distinct divisor and
) is not paired with a distinct divisor and 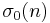 is then odd.
is then odd.
For a prime number p,
because by definition, the factors of a prime number are 1 and itself. Also,where pn# denotes the primorial,
since n prime factors allow a sequence of binary selection (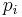 or 1) from n terms for each proper divisor formed.
or 1) from n terms for each proper divisor formed.
Clearly, 1 < d(n) < n and σ(n) > n for all n > 2.
The divisor function is multiplicative, but not completely multiplicative. The consequence of this is that, if we write
where r = ω(n) is the number of distinct prime factors of n, pi is the ith prime factor, and ai is the maximum power of pi by which n is divisible, then we have
which is equivalent to the useful formula:
It follows (by setting x = 0) that d(n) is:
For example, if n is 24, there are two prime factors (p1 is 2; p2 is 3); noting that 24 is the product of 23×31, a1 is 3 and a2 is 1. Thus we can calculate d(24) as so:
The eight divisors counted by this formula are 1, 2, 4, 8, 3, 6, 12, and 24.
We also note s(n) = σ(n) − n. Here s(n) denotes the sum of the proper divisors of n, i.e. the divisors of n excluding n itself. This function is the one used to recognize perfect numbers which are the n for which s(n) = n. If s(n) > n then n is an abundant number and if s(n) < n then n is a deficient number.
If n is a power of 2, e.g. 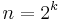 , then
, then 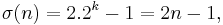 and s(n) = n - 1, which makes n almost-perfect.
and s(n) = n - 1, which makes n almost-perfect.
As an example, for two distinct primes p and q with p < q, let
Then
and
where φ(n) is Euler's totient function.
Then, the roots of:
allows us to express p and q in terms of σ(n) and φ(n) only, without even knowing n or p+q, as:
Also, knowing n and either σ(n) or φ(n) (or knowing p+q and either σ(n) or φ(n)) allows us to easily find p and q.
In 1984, Roger Heath-Brown proved that
- d(n) = d(n + 1)
will occur infinitely often.
Series relations
Two Dirichlet series involving the divisor function are:
which for d(n) = σ0(n) gives
and
A Lambert series involving the divisor function is:
for arbitrary complex |q| ≤ 1 and a. This summation also appears as the Fourier series of the Eisenstein series and the invariants of the Weierstrass elliptic functions.
Approximate growth rate
In little-o notation, the divisor function satisfies the inequality (see page 296 of Apostol’s book[5])
More precisely, Severin Wigert showed that
On the other hand, since there are infinitely many prime numbers,
In Big-O notation, Dirichlet showed that the average order of the divisor function satisfies the following inequality (see Theorem 3.3 of Apostol’s book[5])
where  is Euler's constant. Improving the bound
is Euler's constant. Improving the bound 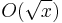 in this formula is known as Dirichlet's divisor problem
in this formula is known as Dirichlet's divisor problem
The behaviour of the sigma function is irregular. The asymptotic growth rate of the sigma function can be expressed by:
where lim sup is the limit superior. This result is Grönwall's theorem, published in 1913 (Grönwall 1913). His proof uses Mertens' 3rd theorem, which says that
where p denotes a prime.
In 1915, Ramanujan proved that under the assumption of the Riemann hypothesis, the inequality:
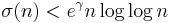 (Robin's inequality)
(Robin's inequality)
holds for all sufficiently large n. In 1984 Guy Robin proved that the inequality is true for all n ≥ 5,041 if and only if the Riemann hypothesis is true (Robin 1984). This is Robin's theorem and the inequality became known after him. The largest known value that violates the inequality is n=5,040. If the Riemann hypothesis is true, there are no greater exceptions. If the hypothesis is false, then Robin showed there are an infinite number of values of n that violate the inequality, and it is known that the smallest such n ≥ 5,041 must be superabundant (Akbary & Friggstad 2009). It has been shown that the inequality holds for large odd and square-free integers, and that the Riemann hypothesis is equivalent to the inequality just for n divisible by the fifth power of a prime (Choie et al. 2007).
A related bound was given by Jeffrey Lagarias in 2002, who proved that the Riemann hypothesis is equivalent to the statement that
for every natural number n, where 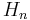 is the nth harmonic number, (Lagarias 2002).
is the nth harmonic number, (Lagarias 2002).
Robin also proved, unconditionally, that the inequality
holds for all n ≥ 3.
See also
- Euler's totient function (Euler's phi function)
- Table of divisors
- Divisor sum convolutions Lists a few identities involving the divisor functions
- Unitary divisor
Notes
- ^ Long (1972, p. 46)
- ^ Pettofrezzo & Byrkit (1970, p. 63)
- ^ Long (1972, p. 46)
- ^ Pettofrezzo & Byrkit (1970, p. 58)
- ^ a b Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR0434929
References
- Akbary, Amir; Friggstad, Zachary (2009), "Superabundant numbers and the Riemann hypothesis", American Mathematical Monthly 116 (3): 273–275, doi:10.4169/193009709X470128, http://webdocs.cs.ualberta.ca/~zacharyf/Papers/superabundant.pdf.
- Bach, Eric; Shallit, Jeffrey, Algorithmic Number Theory, volume 1, 1996, MIT Press. ISBN 0-262-02405-5, see page 234 in section 8.8.
- Caveney, Geoffrey; Nicolas, Jean-Louis; Sondow, Jonathan (2011), "Robin's theorem, primes, and a new elementary reformulation of the Riemann Hypothesis", INTEGERS: the Electronic Journal of Combinatorial Number Theory 11: A33, http://www.integers-ejcnt.org/l33/l33.pdf
- Choie, YoungJu; Lichiardopol, Nicolas; Moree, Pieter; Solé, Patrick (2007), "On Robin's criterion for the Riemann hypothesis", Journal de théorie des nombres de Bordeaux 19 (2): 357–372, arXiv:math.NT/0604314, doi:10.5802/jtnb.591, ISSN 1246-7405, MR2394891, http://jtnb.cedram.org/item?id=JTNB_2007__19_2_357_0
- Grönwall, Thomas Hakon (1913), "Some asymptotic expressions in the theory of numbers", Transactions of the American Mathematical Society 14: 113–122, doi:10.1090/S0002-9947-1913-1500940-6
- Lagarias, Jeffrey C. (2002), "An elementary problem equivalent to the Riemann hypothesis", The American Mathematical Monthly 109 (6): 534–543, doi:10.2307/2695443, ISSN 0002-9890, JSTOR 2695443, MR1908008
- Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: D. C. Heath and Company
- Nicolas, Jean-Louis; Ramanujan, Srinivasa; Robin, Guy (1997), "Highly composite numbers", The Ramanujan Journal. an International Journal Devoted to the Areas of Mathematics Influenced by Ramanujan 1 (2): 119–153, doi:10.1023/A:1009764017495, ISSN 1382-4090, MR1606180
- Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall
- Robin, Guy (1984), "Grandes valeurs de la fonction somme des diviseurs et hypothèse de Riemann", Journal de Mathématiques Pures et Appliquées. Neuvième Série 63 (2): 187–213, ISSN 0021-7824, MR774171
- Weisstein, Eric W., "Divisor Function" from MathWorld.
- Weisstein, Eric W., "Robin's Theorem" from MathWorld.
- Elementary Evaluation of Certain Convolution Sums Involving Divisor Functions PDF of a paper by Huard, Ou, Spearman, and Williams. Contains elementary (i.e. not relying on the theory of modular forms) proofs of divisor sum convolutions, formulas for the number of ways of representing a number as a sum of triangular numbers, and related results.
|
||||||||||||||||||||||
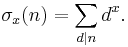
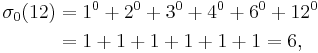
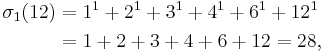
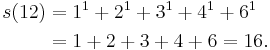
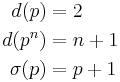
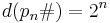
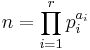
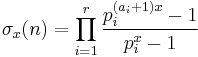
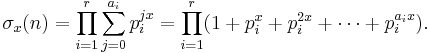
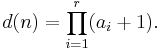
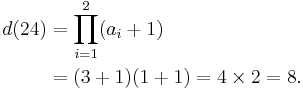
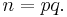
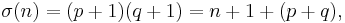
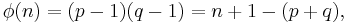
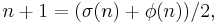
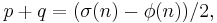
![(x-p)(x-q) = x^2 - (p%2Bq)x %2B n = x^2 - [(\sigma(n) - \phi(n))/2]x %2B [(\sigma(n) %2B \phi(n))/2 - 1] = 0 \,](/2012-wikipedia_en_all_nopic_01_2012/I/e70e85d90a6e3576184171d10c6d531e.png)
![p = (\sigma(n) - \phi(n))/4 - \sqrt{[(\sigma(n) - \phi(n))/4]^2 - [(\sigma(n) %2B \phi(n))/2 - 1]}, \,](/2012-wikipedia_en_all_nopic_01_2012/I/85f47a2d5069d41be60de83f6758d109.png)
![q = (\sigma(n) - \phi(n))/4 %2B \sqrt{[(\sigma(n) - \phi(n))/4]^2 - [(\sigma(n) %2B \phi(n))/2 - 1]}. \,](/2012-wikipedia_en_all_nopic_01_2012/I/c21732c08b6ff1a91662c4fe7417583f.png)